Utah Teapot

Not to be confused with Russell’s Teapot, a cosmic analogy cooked up by the philosopher Bertrand Russell, who evidently had a great sense of humour. Illustrating that the philosophic burden of proof lies upon a person making scientifically unfalsifiable claims, rather than shifting the burden of disproof to others, he famously quipped:

Nobody can prove that there is not between the Earth and Mars a china teapot revolving in an elliptical orbit, but nobody thinks this sufficiently likely to be taken into account in practice. I think the Christian God just as unlikely.

The Utah Teapot is somewhat less exciting. This three-dimensional computer model has inexplicably become a standard reference object in the computer graphics community, something akin to a “hello world” program.

The mathematical data describing the geometry of said teapot was made publicly available by Martin Newell, then a researcher at the University of (surprise surprise) Utah. This household object had basic elements that made it ideal for experiments. It was round with saddle points, had a genus greater than zero, and could even project a shadow onto itself.

A Quick Primer in Topology

A contour line connects points of equal value, given some function. A level set is the generalisation of this to higher dimensions. Imagine a hilly geographical terrain that, tragically, is being flooded with water. The scalar function that describes this terrain is the height function. Contours are curves that are made up of all the points that are at the same height, meaning the result of marking the level of water at a given time all over the terrain.

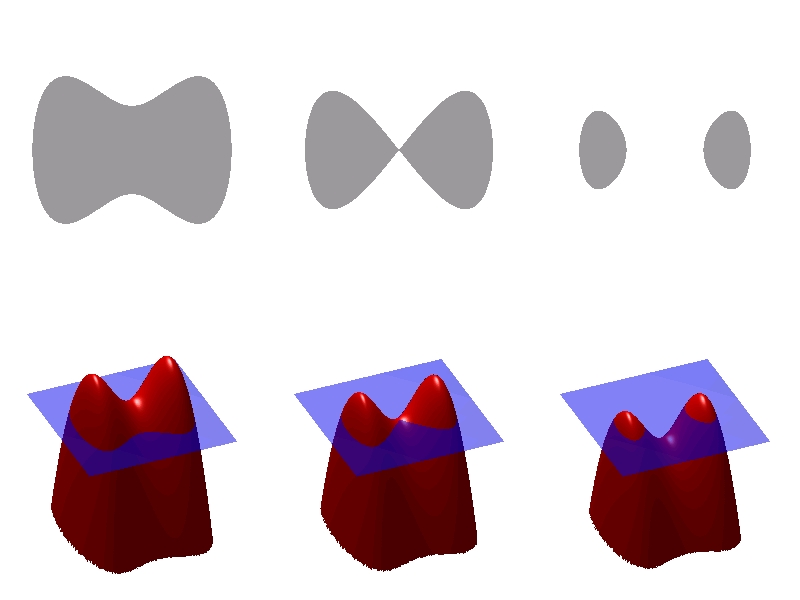
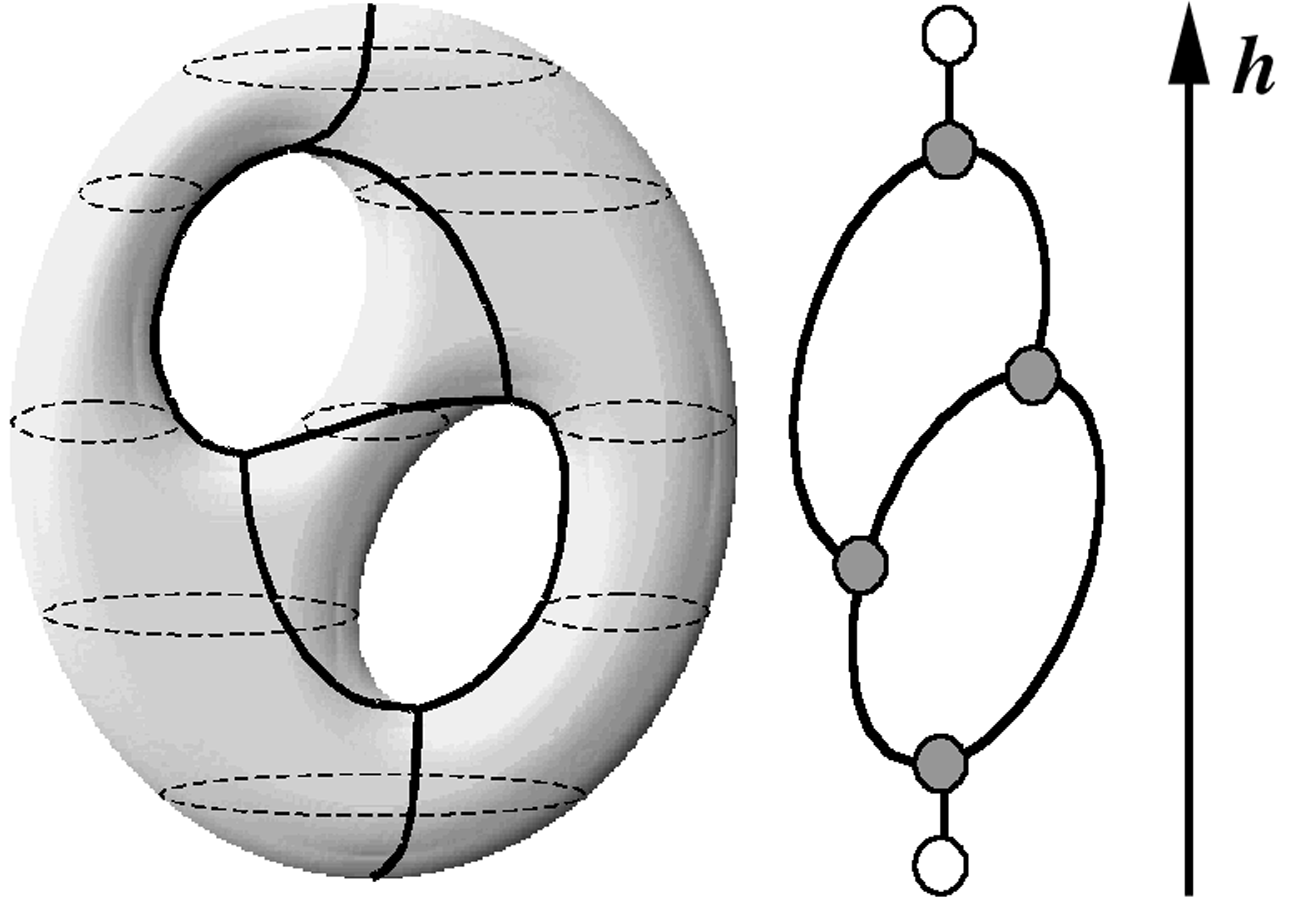
Saddle points are where the slope of the function is zero, despite them not being points of local minimum or maximum. Think of…well, a saddle. So our teapot clearly has a saddle point where the spout meets the body. An orientable surface is one for which at any point, there is only one direction of the normal to the surface. The genus of a connected, orientable surface essentially tells you how many holes are in it. The teapot has a hole in the handle, hence genus greater than zero.

Representing all this information by collapsing connected components into single points results in what is called a contour tree. In case this graph has loops, it is banished from the realm of trees and is called a Reeb graph instead.

Coffee Mugs and Donuts

The motivating insight behind topology is that what matters for some geometric problems is not the exact shape of the objects involved, but rather the way in which they are put together. Two spaces are homeomorphic if one can be deformed into the other, but without any cutting or gluing.

A traditional joke is that a topologist cannot distinguish a coffee mug from a donut, since a sufficiently pliable donut could be reshaped to a coffee cup by creating a dimple and progressively enlarging it, while shrinking the hole into a handle.

Hairy Balls

There is no non-vanishing continuous tangent vector field on a sphere. Or, in plain English, the hairy ball theorem of algebraic topology states:

One cannot comb the hair flat on a hairy ball without creating a cowlick.

If you were paying attention, you’ll note that this in fact applies not just to spheres, but to any kind of smooth blob, as long as it has no holes.

Klein Bottle

Orientable surfaces are dull. Allow me to introduce the Klein bottle. It’s the college version of the middle school party trick Mobius strip, which is also non-orientable.

This limerick by Leo Moser attempts to describe it:

A mathematician named Klein
Thought the Mobius band was divine.
Said he: “If you glue
The edges of two,
You’ll get a weird bottle like mine.”

If your head isn’t hurting, you’re imagining it wrong.